自相关：诊断与处理

楚新元 / 2021-09-05

如果对于不同的样本点，随机误差项之间不再是不相关的，而是存在某种相关性，则认为出现了序列相关性。古扎拉蒂《经济计量学精要》表 10-7 给出的1980 ~ 2006年间股票价格和 GDP 的数据。

数据：https://cxy.rbind.io/source/Table10_7.xls

载入数据

options(digits = 4)
library(readxl)
library(dplyr)
library(kableExtra)
data = read_xls(
  "data/Table10_7.xls", 
  skip = 4, n_max = 27
)[, 2:3]
data %>% 
  kable() %>% 
   kable_styling(
     bootstrap_options = "striped",
     font_size = 14
  )

NYSE	GDP
720.1	2790
782.6	3128
728.8	3255
979.5	3537
977.3	3933
1143.0	4220
1438.0	4463
1709.8	4740
1585.1	5104
1903.4	5484
1939.5	5803
2181.7	5996
2421.5	6338
2639.0	6657
2687.0	7072
3078.6	7398
3787.2	7817
4827.4	8304
5818.3	8747
6546.8	9268
6805.9	9817
6397.9	10128
5578.9	10470
5447.5	10961
6612.6	11686
7349.0	12434
8358.0	13195

建立一元线性回归模型

model = lm(NYSE ~ GDP, data = data)
summary(model)
## 
## Call:
## lm(formula = NYSE ~ GDP, data = data)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##  -1002   -446   -101    323   1404 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -2.02e+03   3.06e+02   -6.58  6.8e-07 ***
## GDP          7.72e-01   3.96e-02   19.52  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 615 on 25 degrees of freedom
## Multiple R-squared:  0.938,	Adjusted R-squared:  0.936 
## F-statistic:  381 on 1 and 25 DF,  p-value: <2e-16

自相关的诊断

观察残差走势

# plot(model, which = 1)
plot(model$residuals)
abline(h = 0, lty = 3)

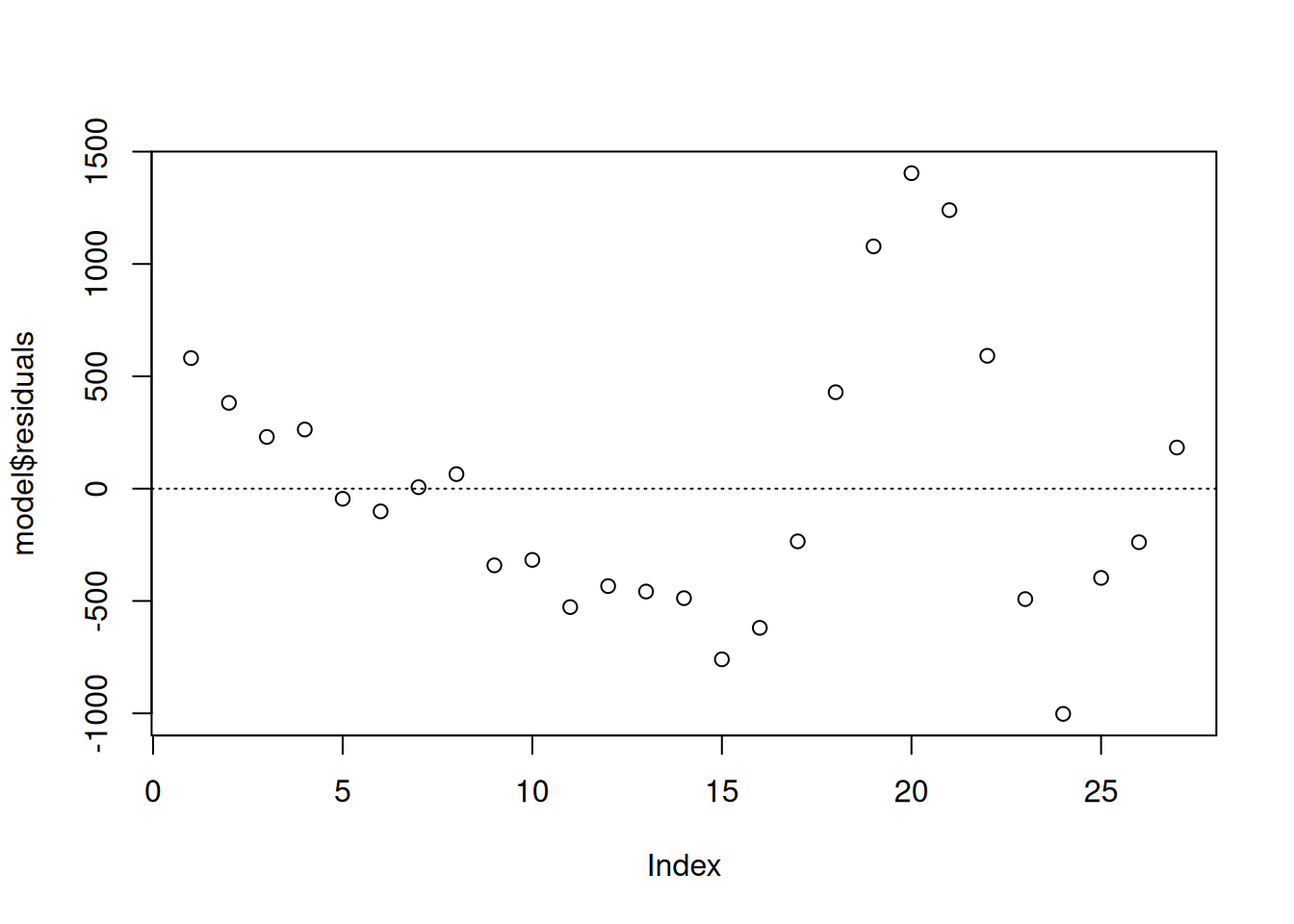
从图中可以看出，残差呈现出有规律的波动，初步判断模型存在自相关。

观察残差和残差滞后一阶的散点图

e = model$residuals
plot(e[-1] ~ e[-nrow(data)], xlab = "e(-1)", ylab = "e")
abline(h = 0, lty = 3)
abline(v = 0, lty = 3)

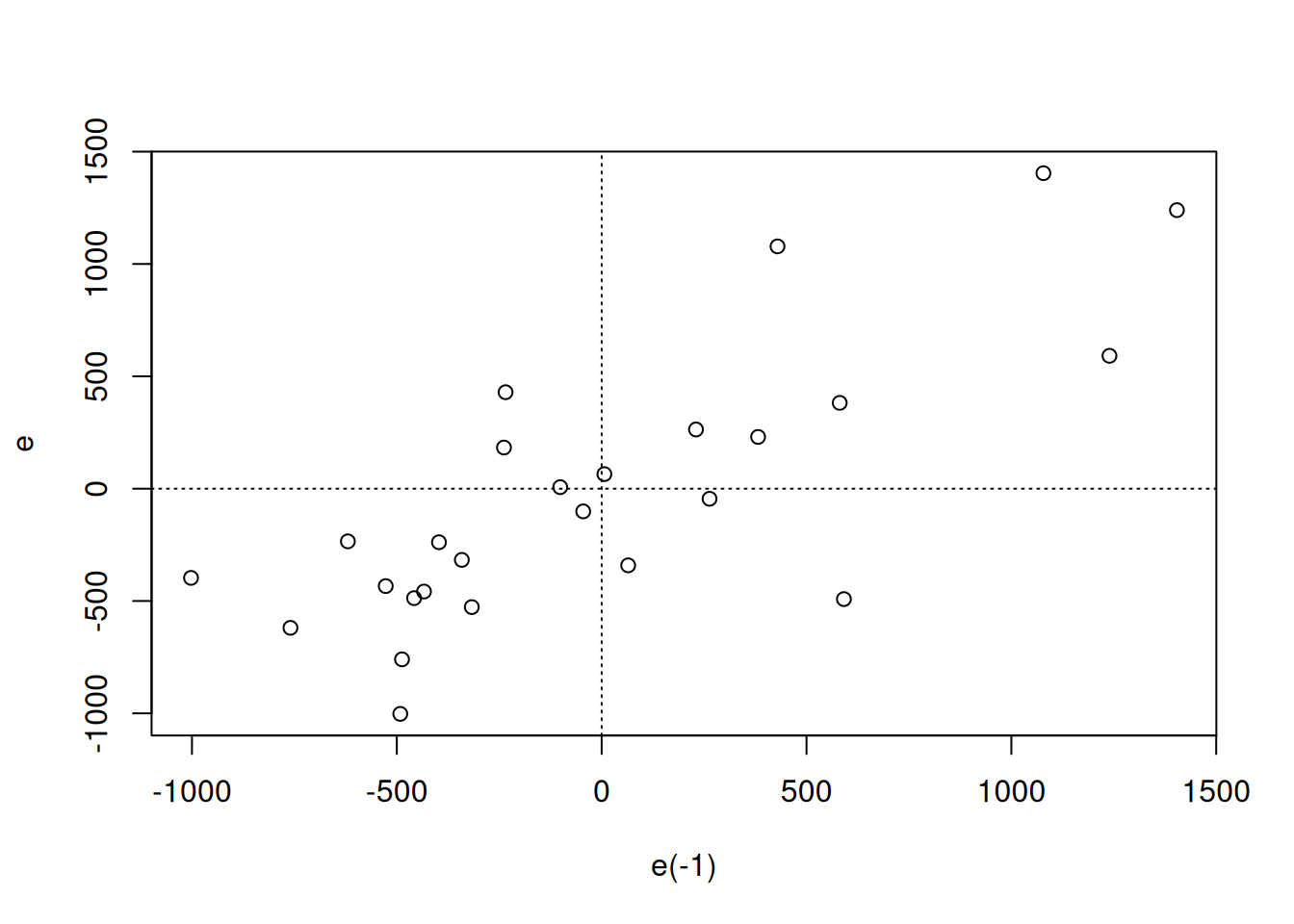
残差滞后一阶和残差散点图上，散点主要分布在一、三象限，初步判断模型存在正自相关。

自相关图

acf(data$NYSE)

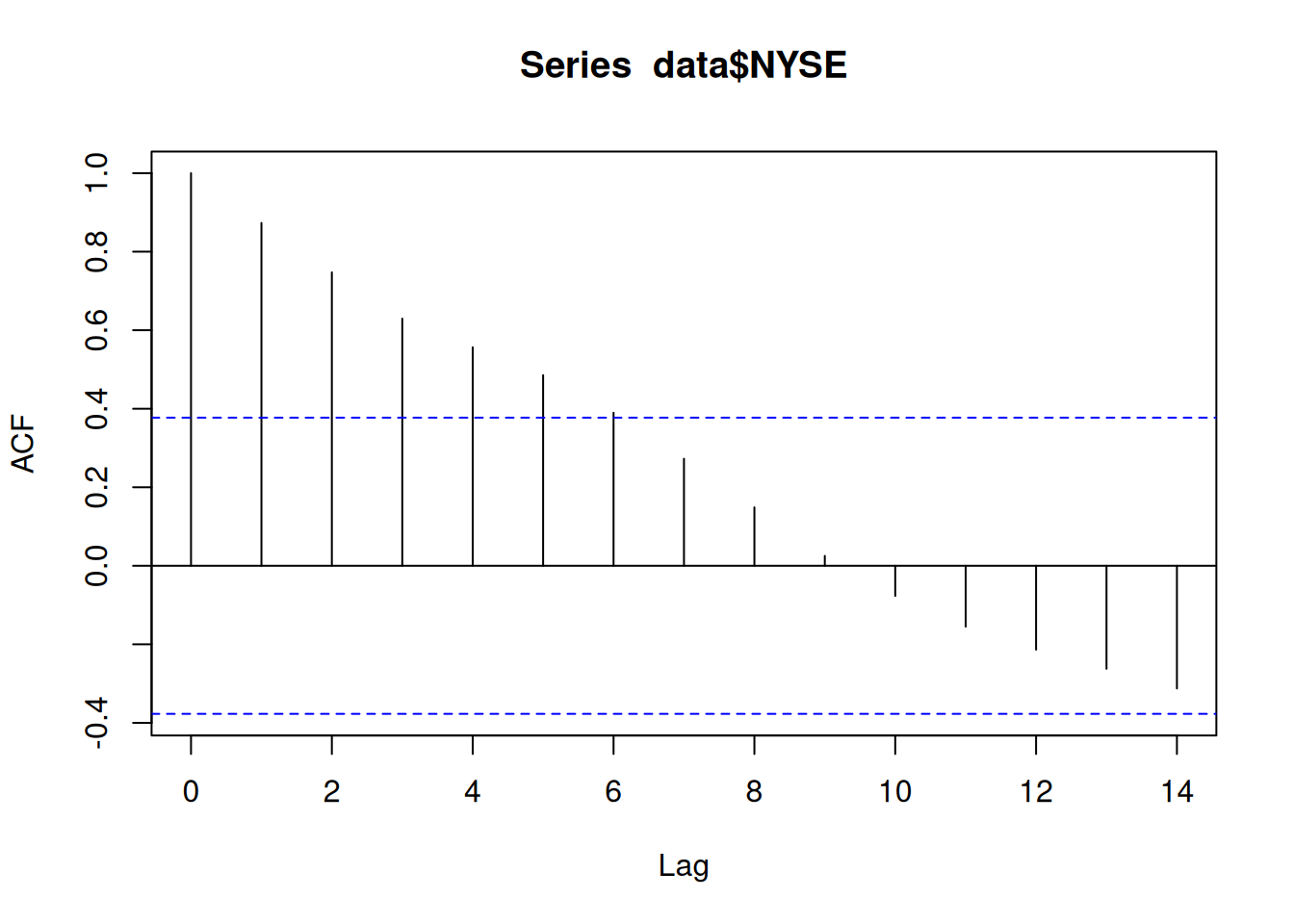
DW 一阶自相关检验

library(lmtest)
dwtest(model)
## 
## 	Durbin-Watson test
## 
## data:  model
## DW = 0.43, p-value = 2e-08
## alternative hypothesis: true autocorrelation is greater than 0

当 n = 27, k’ = 1时，显著性水平为 5% 的 DW 统计量临界值为 1.316 和 1.469。因为 DW 统计量的值为 0.4285，小于 1.316，因此模型存在正一阶自相关。

LM 检验

bgtest(model)
## 
## 	Breusch-Godfrey test for serial correlation of order up to 1
## 
## data:  model
## LM test = 16, df = 1, p-value = 7e-05

LM 检验拒绝无自相关原假设，表明模型存在自相关。

ρ 值通过 DW 值估计得到，用 OLS 估计广义差分方程

根据 DW 值计算 ρ 值

ρ_hat_dw = 1 - dwtest(model)$statistic / 2
names(ρ_hat_dw) = "ρ_hat_dw"
print(ρ_hat_dw)
## ρ_hat_dw 
##    0.7858

估计原模型的 `$\beta_{1}$` 和 `$\beta_{2}$` (舍去第一个观测值)

data %>%
  mutate(
    NYSE_star = NYSE - ρ_hat_dw * lag(NYSE, 1),  # 此处lag是滞后的意思
    GDP_star = GDP - ρ_hat_dw * lag(GDP, 1)
  ) %>%
  na.omit() %>%
  lm(NYSE_star ~ GDP_star, data = .) -> model_star_lack
  # 此处差分损失一个样本。
  # 如果样本量足够多，可以不用补齐第一个缺失值。
  # 如果样本量小，可以通过sqrt(1-ρ^2)*Y[1]、sqrt(1-ρ^2)*X[1]补齐。

beta1_lack = coef(model_star_lack)[1] / (1 - ρ_hat_dw)
beta2_lack = coef(model_star_lack)[2]
names(beta2_lack) = "GDP"

summary(model_star_lack)
## 
## Call:
## lm(formula = NYSE_star ~ GDP_star, data = .)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -996.2 -150.5   22.8  177.6  727.0 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -617.954    205.309   -3.01   0.0061 ** 
## GDP_star       0.862      0.102    8.47  1.1e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 378 on 24 degrees of freedom
## Multiple R-squared:  0.749,	Adjusted R-squared:  0.739 
## F-statistic: 71.7 on 1 and 24 DF,  p-value: 1.14e-08

# 利用 DW-test 对 model_star_lack 模型进行检验
dwtest(model_star_lack)
## 
## 	Durbin-Watson test
## 
## data:  model_star_lack
## DW = 0.91, p-value = 5e-04
## alternative hypothesis: true autocorrelation is greater than 0

# 利用 LM-test 对 model_star_lack 模型进行检验
bgtest(model_star_lack)
## 
## 	Breusch-Godfrey test for serial correlation of order up to 1
## 
## data:  model_star_lack
## LM test = 7.6, df = 1, p-value = 0.006

还原后的估计方程： $$ \widehat{NYSE} = -2884.2875 + 0.8624 * GDP $$

估计原模型的 `$\beta_{1}$` 和 `$\beta_{2}$` (包含第一个观测值)

data %>%
  mutate(
    NYSE_star = NYSE - ρ_hat_dw * lag(NYSE, 1), 
    GDP_star = GDP - ρ_hat_dw * lag(GDP, 1),
    NYSE_star_1 = sqrt(1-ρ_hat_dw^2) * NYSE * c(1,rep(0,nrow(data)-1)),
    GDP_star_1 = sqrt(1-ρ_hat_dw^2) * GDP * c(1,rep(0,nrow(data)-1))
  ) -> data_NA

data_NA$NYSE_star[is.na(data_NA$NYSE_star)] = 0
data_NA$GDP_star[is.na(data_NA$GDP_star)] = 0
    
data_NA %>%
  mutate(
    NYSE_star_full = NYSE_star + NYSE_star_1,
    GDP_star_full = GDP_star + GDP_star_1
  ) %>%
  lm(
    NYSE_star_full ~ GDP_star_full, 
    data = .
  ) -> model_star_full

beta1_full = coef(model_star_full)[1] / (1 - ρ_hat_dw)
beta2_full = coef(model_star_full)[2]
names(beta2_full) = "GDP"

summary(model_star_full)
## 
## Call:
## lm(formula = NYSE_star_full ~ GDP_star_full, data = .)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -983.4 -179.8   37.8  194.1  741.1 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -642.233    204.978   -3.13   0.0044 ** 
## GDP_star_full    0.867      0.102    8.48  7.9e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 380 on 25 degrees of freedom
## Multiple R-squared:  0.742,	Adjusted R-squared:  0.732 
## F-statistic:   72 on 1 and 25 DF,  p-value: 7.91e-09

# 利用 DW-test 对 model_star_full 模型进行检验
dwtest(model_star_full)
## 
## 	Durbin-Watson test
## 
## data:  model_star_full
## DW = 0.92, p-value = 5e-04
## alternative hypothesis: true autocorrelation is greater than 0

# 利用 LM-test 对 model_star_full 模型进行检验
bgtest(model_star_full)
## 
## 	Breusch-Godfrey test for serial correlation of order up to 1
## 
## data:  model_star_full
## LM test = 7, df = 1, p-value = 0.008

还原后的估计方程： $$ \widehat{NYSE} = -2997.6114 + 0.867 * GDP $$

ρ 值通过 OLS 残差估计得到

根据 OLS 残差估计 ρ 值

uxfit = lm(
  model$residuals ~ 0 + lag(model$residuals), 
  data = data
)
ρ_hat_ols = coef(uxfit)[1]
names(ρ_hat_ols) = "ρ_hat_ols"
print(ρ_hat_ols)
## ρ_hat_ols 
##     0.7689

估计原模型的 `$\beta_{1}$` 和 `$\beta_{2}$` (舍去第一个观测值)

data %>%
  mutate(
    NYSE_star = NYSE - ρ_hat_ols * lag(NYSE, 1),
    GDP_star = GDP - ρ_hat_ols * lag(GDP, 1)
  ) %>%
  na.omit() %>%
  lm(
    NYSE_star ~ GDP_star, 
    data = .
  ) -> model_star_lack2
  # 此处差分损失一个样本。
  # 如果样本量足够多，可以不用补齐第一个缺失值。
  # 如果样本量小，可以通过sqrt(1-ρ^2)*Y[1]、sqrt(1-ρ^2)*X[1]补齐。

beta1_lack2 = coef(model_star_lack2)[1] / (1 - ρ_hat_ols)
beta2_lack2 = coef(model_star_lack2)[2]
names(beta2_lack2) = "GDP"

summary(model_star_lack2)
## 
## Call:
## lm(formula = NYSE_star ~ GDP_star, data = .)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -985.7 -149.8   21.5  178.3  735.0 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -647.2103   205.0171   -3.16   0.0043 ** 
## GDP_star       0.8547     0.0957    8.93  4.3e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 379 on 24 degrees of freedom
## Multiple R-squared:  0.769,	Adjusted R-squared:  0.759 
## F-statistic: 79.7 on 1 and 24 DF,  p-value: 4.29e-09

# 利用 DW-test 对 model_star_lack2 模型进行检验
dwtest(model_star_lack2)
## 
## 	Durbin-Watson test
## 
## data:  model_star_lack2
## DW = 0.9, p-value = 4e-04
## alternative hypothesis: true autocorrelation is greater than 0

# 利用 LM-test 对 model_star_lack2 模型进行检验
bgtest(model_star_lack2)
## 
## 	Breusch-Godfrey test for serial correlation of order up to 1
## 
## data:  model_star_lack2
## LM test = 7.8, df = 1, p-value = 0.005

还原后的估计方程： $$ \widehat{NYSE} = -2800.1965 + 0.8547 * GDP $$

估计原模型的 `$\beta_{1}$` 和 `$\beta_{2}$` (包含第一个观测值)

data %>%
  mutate(
    NYSE_star = NYSE - ρ_hat_ols * lag(NYSE, 1), 
    GDP_star = GDP - ρ_hat_ols * lag(GDP, 1),
    NYSE_star_1 = sqrt(1-ρ_hat_ols^2) * NYSE * c(1,rep(0,nrow(data)-1)),
    GDP_star_1 = sqrt(1-ρ_hat_ols^2) * GDP * c(1,rep(0,nrow(data)-1))
  ) -> data_NA2

data_NA2$NYSE_star[is.na(data_NA2$NYSE_star)] = 0
data_NA2$GDP_star[is.na(data_NA2$GDP_star)] = 0

data_NA2 %>%
  mutate(
    NYSE_star_full = NYSE_star + NYSE_star_1,
    GDP_star_full = GDP_star + GDP_star_1
  ) %>%
  lm(
    NYSE_star_full ~ GDP_star_full, 
    data = .
  ) -> model_star_full2

b1_full2 = coef(model_star_full2)[1] / (1 - ρ_hat_ols)
b2_full2 = coef(model_star_full2)[2]
names(b2_full2) = "GDP"

summary(model_star_full2)
## 
## Call:
## lm(formula = NYSE_star_full ~ GDP_star_full, data = .)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -974.1 -180.7   36.1  194.2  748.4 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -673.4730   204.2343   -3.30   0.0029 ** 
## GDP_star_full    0.8601     0.0959    8.97  2.8e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 380 on 25 degrees of freedom
## Multiple R-squared:  0.763,	Adjusted R-squared:  0.753 
## F-statistic: 80.4 on 1 and 25 DF,  p-value: 2.75e-09

# 利用 DW-test 对 model_star_full2 模型进行检验
dwtest(model_star_full2)
## 
## 	Durbin-Watson test
## 
## data:  model_star_full2
## DW = 0.92, p-value = 4e-04
## alternative hypothesis: true autocorrelation is greater than 0

# 利用 LM-test 对 model_star_full2 模型进行检验
bgtest(model_star_full2)
## 
## 	Breusch-Godfrey test for serial correlation of order up to 1
## 
## data:  model_star_full2
## LM test = 7.2, df = 1, p-value = 0.007

还原后的估计方程： $$ \widehat{NYSE} = -2913.8235 + 0.8601 * GDP $$

利用一阶差分法对变换后的模型进行估计

data %>%
  mutate(
    NYSE_star = NYSE - lag(NYSE, 1),
    GDP_star = GDP - lag(GDP, 1)
  ) %>%
  na.omit() %>%
  lm(
    NYSE_star ~ 0 + GDP_star,
    data = .
  ) -> model_star_3

beta2_3 = coef(model_star_3)
names(beta2_3) = "GDP"
beta1_3 = mean(data$NYSE) - beta2_3 * mean(data$GDP)
names(beta1_3 ) = "Intercept"

summary(model_star_3)
## 
## Call:
## lm(formula = NYSE_star ~ 0 + GDP_star, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1115.6  -238.5   -34.7   103.3   616.9 
## 
## Coefficients:
##          Estimate Std. Error t value Pr(>|t|)    
## GDP_star    0.868      0.183    4.75  7.1e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 401 on 25 degrees of freedom
## Multiple R-squared:  0.474,	Adjusted R-squared:  0.453 
## F-statistic: 22.6 on 1 and 25 DF,  p-value: 7.14e-05

# 利用 LM-test 对 model_star_3 模型进行检验
bgtest(model_star_3)
## 
## 	Breusch-Godfrey test for serial correlation of order up to 1
## 
## data:  model_star_3
## LM test = 7.1, df = 1, p-value = 0.008

还原后的估计方程： $$ \widehat{NYSE} = -2701.4792 + 0.8684 * GDP $$

自相关：诊断与处理

楚新元 / 2021-09-05

载入数据

建立一元线性回归模型

自相关的诊断

观察残差走势

观察残差和残差滞后一阶的散点图

自相关图

DW 一阶自相关检验

LM 检验

ρ 值通过 DW 值估计得到，用 OLS 估计广义差分方程

根据 DW 值计算 ρ 值

估计原模型的 `\(\beta_{1}\)` 和 `\(\beta_{2}\)` (舍去第一个观测值)

估计原模型的 `\(\beta_{1}\)` 和 `\(\beta_{2}\)` (包含第一个观测值)

ρ 值通过 OLS 残差估计得到

根据 OLS 残差估计 ρ 值

估计原模型的 `\(\beta_{1}\)` 和 `\(\beta_{2}\)` (舍去第一个观测值)

估计原模型的 `\(\beta_{1}\)` 和 `\(\beta_{2}\)` (包含第一个观测值)

利用一阶差分法对变换后的模型进行估计

载入数据

建立一元线性回归模型

自相关的诊断

观察残差走势

观察残差和残差滞后一阶的散点图

自相关图

DW 一阶自相关检验

LM 检验

ρ 值通过 DW 值估计得到，用 OLS 估计广义差分方程

根据 DW 值计算 ρ 值

估计原模型的 \(\beta_{1}\) 和 \(\beta_{2}\) (舍去第一个观测值)

估计原模型的 \(\beta_{1}\) 和 \(\beta_{2}\) (包含第一个观测值)

ρ 值通过 OLS 残差估计得到

根据 OLS 残差估计 ρ 值

估计原模型的 \(\beta_{1}\) 和 \(\beta_{2}\) (舍去第一个观测值)

估计原模型的 \(\beta_{1}\) 和 \(\beta_{2}\) (包含第一个观测值)

利用一阶差分法对变换后的模型进行估计

估计原模型的 `\(\beta_{1}\)` 和 `\(\beta_{2}\)` (舍去第一个观测值)

估计原模型的 `\(\beta_{1}\)` 和 `\(\beta_{2}\)` (包含第一个观测值)

估计原模型的 `\(\beta_{1}\)` 和 `\(\beta_{2}\)` (舍去第一个观测值)

估计原模型的 `\(\beta_{1}\)` 和 `\(\beta_{2}\)` (包含第一个观测值)